Teaching
Stochastic Processes, Spring 2019
https://bellecp.github.io/teaching/2019-Spring-Stochastic-Processes/
TA: Chencheng Cai, chencheng.cai@rutgers.edu. Office hours: Monday 3pm-4.30pm and Thursday 3pm-4.30pm, Hill Center 450.
Prof: Pierre C Bellec, pierre.bellec@rutgers.edu. Office hours: Wednesday 10.30am-12.00, Hill Center 406.
- Stochastic Processes, Spring 2019
- Send (anonymous) comments/suggestions on the course
- Exams
- Grading
- Book(s)
- Tentative syllabus, subject to change
- Lecture notes from class
- Homework, Midterm solutions
- Homeworks
- Some pictures
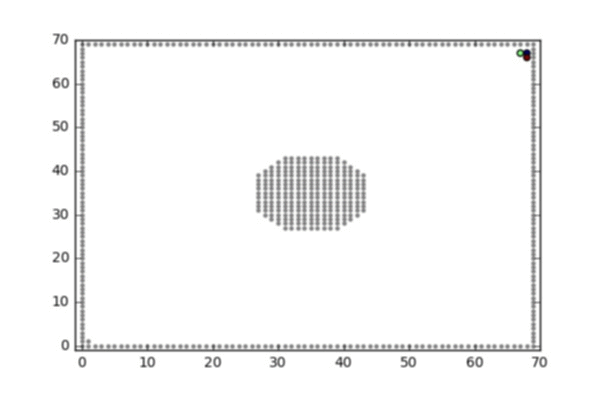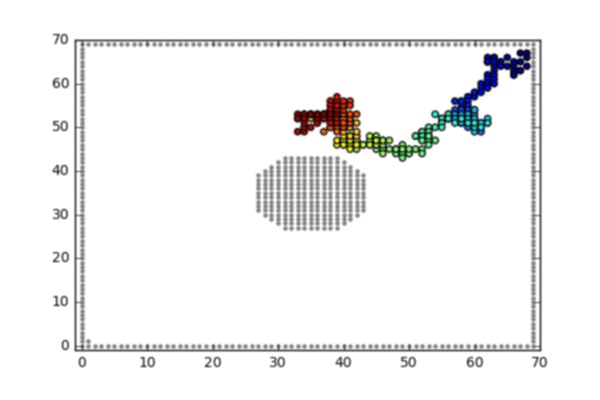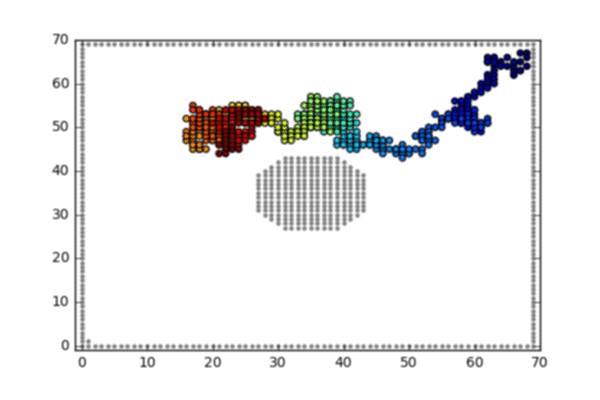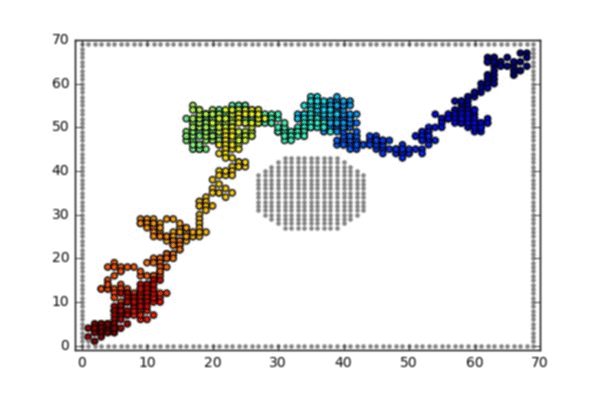
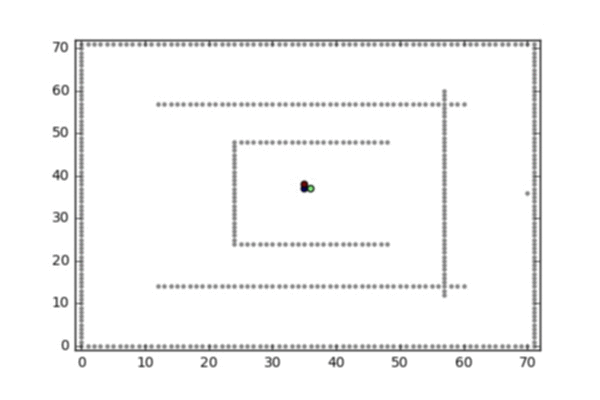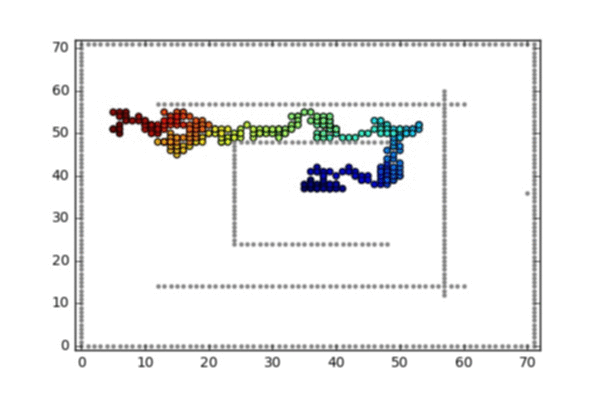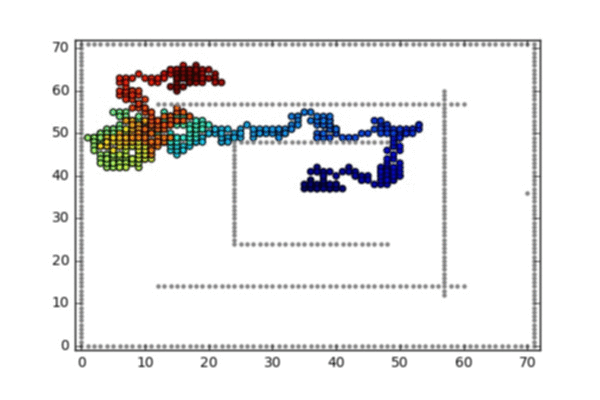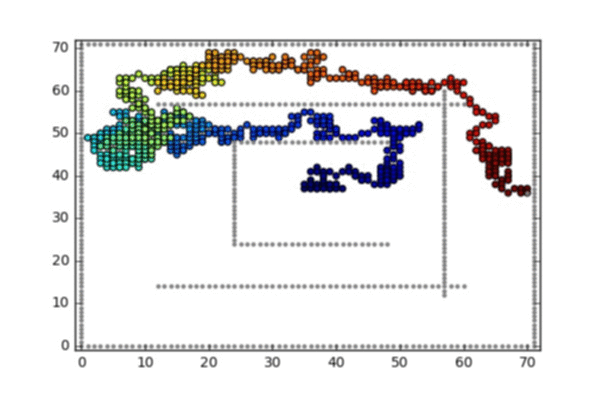
- A random walk on the 2d lattice conditioned on hitting the bottom left corner before hitting the square boundaries or the obstacle in the middle
- A random walk on the 2d lattice conditioned on hitting the single point on the right before hitting the square boundaries or maze walls
- Glauber dynamics on hardcore configurations:
- The pivot chain on self-avoiding paths:
Send (anonymous) comments/suggestions on the course
https://goo.gl/forms/RX6vt5PN2wcuVHHr1
Exams
- First Midterm: March 4 in class.
- Final: TBA
Grading
- Final: 50 percent
- Midterms: 25 percent each
- Homework and other take-home assignments: 25 percent
Book(s)
- For Markov chains, mixing times and martingales: the book by DA Levin, Y Peres, and EL Wilmer. It is available at http://pages.uoregon.edu/dlevin/MARKOV/mcmt2e.pdf. Make sure to download the PDF from this URL, as this URL contains an updated book with some typos/errors fixed.
- For Poisson processes and renewal theory, the notes from class are written at https://www.overleaf.com/read/mhqvnwtfdfgw
We will start the semester with Markov chains and the first book.
Prerequisites on Probability Theory
For prerequisites on probability, you may also look at Appendix 1 in DA Levin, Y Peres, and EL Wilmer. You may look at Chapter 1 in Ross.
Tentative syllabus, subject to change
- From the DA Levin, Y Peres, and EL Wilmer book: Chapters 1, 2, 3, 4, 5, 7. Time permitting: Chapters 8, 9, 10, 11, 17, 18.
- Poisson Processes and renewal theory: TBA
Lecture notes from class
https://1drv.ms/f/s!AqJw0uotmkduhQIhCLqaXeuHK7A_
Homework, Midterm solutions
TBA
Homeworks
Due to a large class size and time constraints, not all exercises will be graded.
Homework sources
If you would like to type your answers in latex/pandoc/etc, the sources of the homework PDF are available
at https://bellecp.github.io/teaching/2019-Spring-Stochastic-Processes/hw-sources.zip.
For instance, you can write your answers after each question in the .md file.
A .md file can be compiled into pdf using ``pandoc`, https://pandoc.org/installing.html.
Homework 1 due Monday Jan 28
https://bellecp.github.io/teaching/2019-Spring-Stochastic-Processes/homework1v2.pdf
Homework 2 due Monday Feb 4
https://bellecp.github.io/teaching/2019-Spring-Stochastic-Processes/homework2.pdf
Homework 3 due Monday Feb 18
https://bellecp.github.io/teaching/2019-Spring-Stochastic-Processes/homework3.pdf
Homework 4 due Monday Feb 25
https://bellecp.github.io/teaching/2019-Spring-Stochastic-Processes/homework4v2.pdf
No homework 5 due to midterm
Homework 6 due Monday March 11
https://bellecp.github.io/teaching/2019-Spring-Stochastic-Processes/homework6.pdf
Homework 7 due Monday March 25
https://bellecp.github.io/teaching/2019-Spring-Stochastic-Processes/homework7.pdf
Spring break take-home assignment, due April 8
https://bellecp.github.io/teaching/2019-Spring-Stochastic-Processes/take-home.pdf
Homework 8 due April 29
https://bellecp.github.io/teaching/2019-Spring-Stochastic-Processes/homework9.pdf
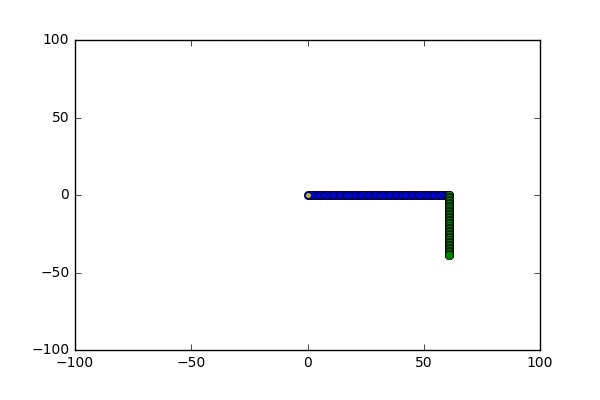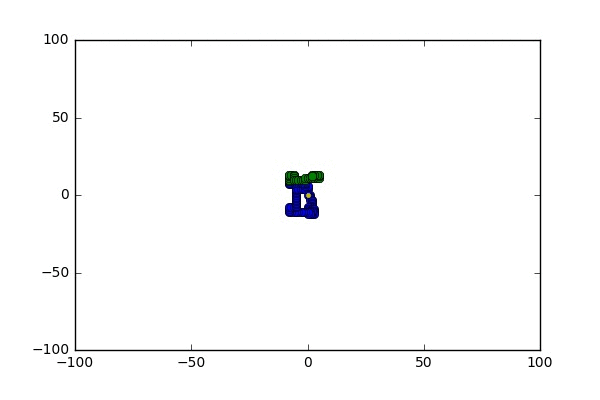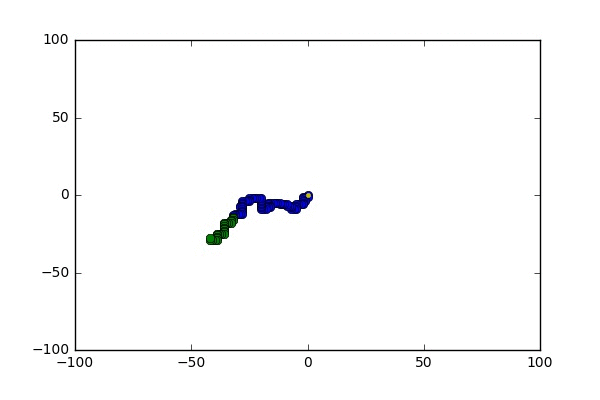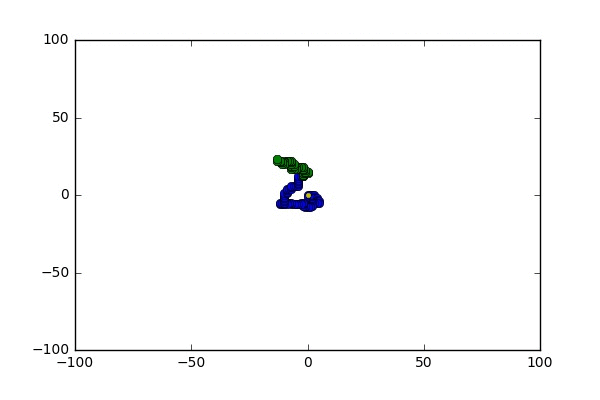
Some pictures
A random walk on the 2d lattice conditioned on hitting the bottom left corner before hitting the square boundaries or the obstacle in the middle
A random walk on the 2d lattice conditioned on hitting the single point on the right before hitting the square boundaries or maze walls
Glauber dynamics on hardcore configurations:
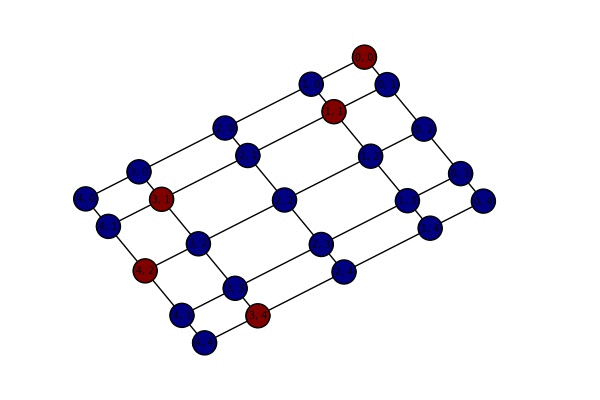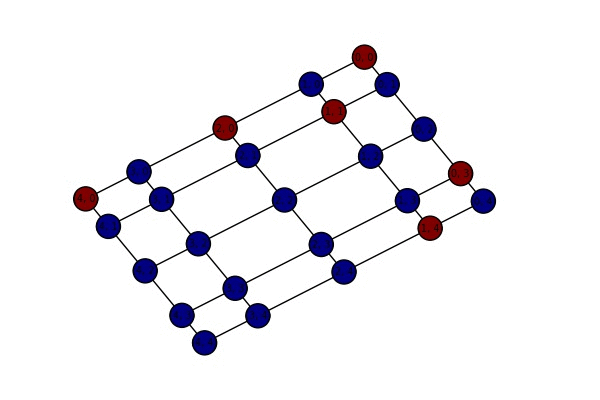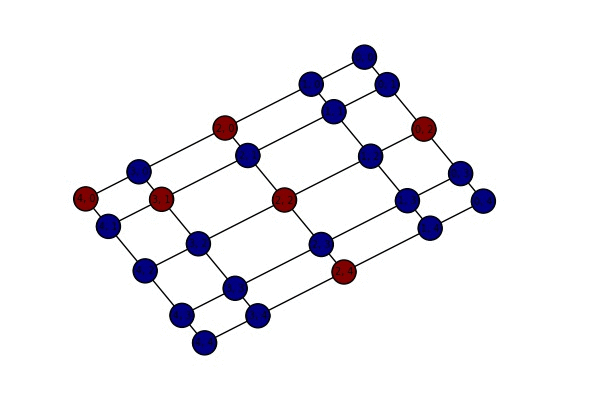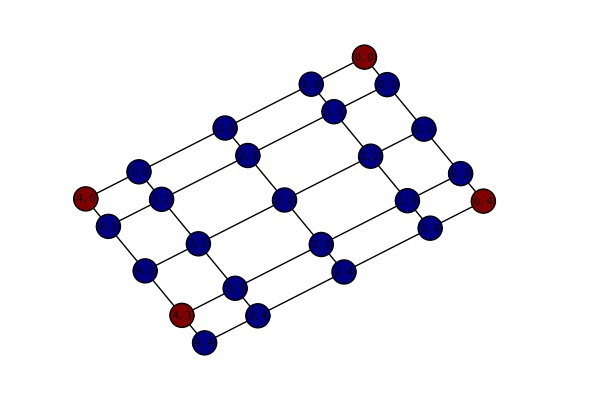
The pivot chain on self-avoiding paths: